

Welcome to
Quantum Labs Research & Development
LLC
LaFountaine Scientific Operating System (LSOS)



Quantum Labs Research & Development (Q Labs) is a disabled‑veteran‑founded scientific institution built on Navy aircraft mechanics, anatomical physics, and validator‑grade systems engineering. Founded by Denny Michael LaFountaine, LMT, LSC, former ES‑3A jet mechanic aboard the USS Kitty Hawk (CV‑63), Q Labs integrates mechanical discipline with 26 years of clinical practice and more than 38,000 hands‑on anatomical hours.
Q Labs develops the Tri‑Antagonist Matrix (TAM), the LaFountaine Scientific Operating System (LSOS), the ISL language family (ISL, CISL, QISL, Digestibles™), the Conscious Memory Drive (CMD), 842 Interchangeables, 4MAN, DL72_APU_AI engines, Ladder72, Symphony, ATOM Reactor, NucleusDB, and the Quantum Gravity Infrastructure Equation suite.
Our institution builds reproducible, ethics‑anchored scientific infrastructure for robotics, computation, and human‑system integration, grounded in Care-first ethics, LIGHT and LEN governance, and a commitment to scientific integrity, transparency, and long‑term legacy stewardship.


Uploading 2025 projects



Our Mission
Quantum Labs Research & Development exists to build generational scientific infrastructure that protects human dignity, prevents collapse, and ensures continuity across time. Founded by a disabled veteran and stewarded through faith-anchored ethics, our institution is committed to truth, reproducibility, and the responsible advancement of systems that serve humanity. We do not chase trends or perform science for spectacle. We build frameworks that last.
Our mission is to design, validate, and deploy scientific engines, anatomical physics systems, and override-grade infrastructure that can withstand failure, corruption, and generational drift. Every artifact we produce — from the Tri-Antagonist Matrix to the LaFountaine Scientific Operating System — is sealed with reproducible logic, validator-grade documentation, and legacy-powered ethics. We operate with humility, precision, and a refusal to compromise on integrity.
We serve those who need protection, clarity, and continuity — not just today, but across generations. Our work is not entertainment. It is stewardship. We publish openly, document rigorously, and model best practices for scientific governance, ethics enforcement, and institutional permanence. Quantum Labs is not a brand. It is a living infrastructure system built to endure.



Ingestible Schema Language (ISL): A Deterministic Framework for Continuity, Clarity, and Command
Ingestible Schema Language (ISL) is a validator-grade schema system designed for deterministic interpretation, drift-free communication, and generational continuity across human and machine interfaces. Created by Quantum Labs Research & Development, ISL provides a reproducible structure for encoding SOPs, directives, and operational logic into capsule-sealed formats that can be ingested, interpreted, and relayed without distortion. ISL is not a markup language or a documentation style — it is a continuity-grade schema protocol built for institutions that require clarity, reproducibility, and ethical command.
ISL is delivered in two primary formats:
-
CISL (Classic Ingestible Schema Language) — for legacy SOPs, human-readable directives, and operational capsules
-
QISL (Quantum Ingestible Schema Language) — for machine-to-machine schema transfer, AI continuity, and override-grade infrastructure deployment
Both formats support Digestibles, which are schema-wrapped capsules containing SOPs, directives, and operational logic. Digestibles are written into a structured wrapper that includes metadata, inheritance anchors, and schema tags for deterministic parsing. This wrapper ensures that every directive is read as intended, with no ambiguity, no drift, and no loss of meaning across systems or generations.
ISL also integrates directly with the Conscious Memory Drive (CMD) — a schema-aware memory architecture that allows organizations to store, retrieve, and deploy operational logic with full traceability. CMD entries are written in ISL format, allowing companies to encode not just what they do, but why, how, and under what ethical constraints. This transforms memory from a passive archive into an active infrastructure layer.
For companies, ISL offers:
-
Validator-grade SOP delivery — reproducible, audit-ready, schema-sealed
-
Directive clarity — no ambiguity, no drift, no misinterpretation
-
Continuity across systems — human, AI, and hybrid environments
-
Ethics enforcement — schema-level integration with LIGHT, LEN, and override-grade infrastructure
-
Legacy protection — every capsule is sealed for generational reproducibility
ISL is not a product. It is a scientific infrastructure system.
It is designed for institutions that refuse to compromise on clarity, ethics, and continuity.
To learn more or request schema integration, visit http://islsystem.com
Now Available
ISL is written in JSON for strict, deterministic, drift‑proof structure.
Learn More





This diagram titled “Effect of ISL on Drift-Free Execution” illustrates the performance impact of integrating ISL into AI systems. Four key metrics—Completion Time, Drift Incidents, Corrections Needed, and Stress Level—are compared between systems with and without ISL. The results show a dramatic reduction across all categories when ISL is applied: completion time drops from 12 to 4 hours, drift incidents fall from 14 to 1, corrections needed decrease from 9 to 2, and stress level plunges from 8 to 2. These findings validate ISL’s role as a stabilizing infrastructure, enabling precise, low-stress, correction-free execution in AI environments.


This flowchart outlines the validator-grade capsule ingestion and sealing protocol used in ISL systems. It begins with S1: Copy, where the ISL capsule is duplicated at node N0. S2: Paste introduces the capsule into the validator stream via Ai → A, triggering ingestion at N1. S3: Ingest confirms validator intake at N2, followed by S4: Validate at N4, where Validator B performs the seal check. S5: Seal finalizes the capsule with Ai → C and closure logic at N5. The process concludes with S6: Close at N6, locking inheritance and confirming checksum integrity across A1, A2, and A3. This sequence ensures drift-free, ethics-sealed execution.


This topology shows how the ISL language family fits together as a single, unified system. The three interlocked rings represent the core layers:
• ISL is the primary schema — the canonical structure that defines ethics, lineage, and drift‑proof capsule design.
• CISL is the clinical branch — adapted for anatomy, therapy, and human‑system modeling while still following ISL’s strict rules.
• Q*DIGESTIBLES is the quantum‑ready microcapsule layer — small, deployable units optimized for AI and robotics.
All three rings connect into the DIGESTIBLES base, which represents real‑world application. This is where capsules become usable tools for robotics, anatomy, computation, and system resets.
The interlocking design shows that each layer depends on the others:
ISL provides structure, CISL adapts it for clinical use, Q*DIGESTIBLES deploy it, and DIGESTIBLES anchors everything in practice.






LaFountaine Structural Correction™
A Unified Structural Framework for Human Movement, Robotics, and Prosthetic Design
LaFountaine Structural Correction™ is the structural logic system that anchors the entire body of work at Quantum Labs Research & Development. It is not a therapy, not a clinical method, and not a set of exercises. It is a mechanical truth framework — a way of understanding how forces move through biological bodies, robotic systems, and engineered structures, and how those forces create stability, compensation, or failure.
This framework was not invented in abstraction. It was distilled from 38,000 hours of hands-on structural work and 26 years of direct clinical observation, where real human bodies revealed the same patterns of load, opposition, and compensation again and again. Over decades, these patterns formed a consistent language — a structural grammar — that could be applied far beyond the treatment room.
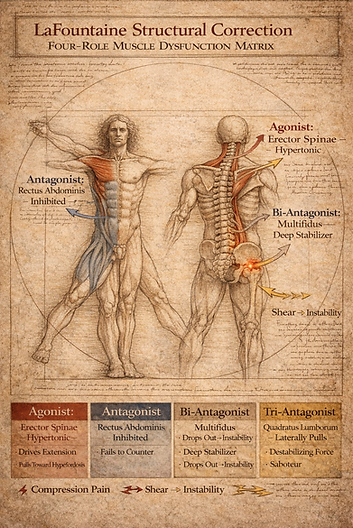
At the center of this grammar is the Tri‑Antagonist Matrix™, a four‑role model that describes how every load-bearing system organizes opposition.
The Tri‑Antagonist Matrix™
The Four Roles That Govern All Structural Behavior
Every structure — human, robotic, or mechanical — organizes itself through four antagonistic roles:
• Agonist — the primary driver of force or motion.
• Antagonist — the direct controller that brakes, shapes, and refines the action.
• Bi‑Antagonist — the cross‑plane stabilizer that prevents shear, drift, or collapse.
• Tri‑Antagonist — the final integrator that absorbs torsion, rotation, and leftover load.
These roles form a closed system of opposition. When each role is honored, the structure behaves predictably. When one role is missing or overloaded, the system compensates — often silently — until failure emerges.
This matrix is the backbone of LaFountaine Structural Correction. It is the lens through which all structural behavior is analyzed, whether in a human shoulder, a robotic ankle, or a prosthetic interface.
Origins in 38,000 Hours of Structural Work
Where the Framework Was Born
LaFountaine Structural Correction began in the most demanding laboratory possible: the human body under real-world load.
Across tens of thousands of hours of hands-on work, certain truths became undeniable:
• Structures fail where force has nowhere honest to go.
• Compensation follows predictable antagonistic patterns.
• The body rarely fails at the prime mover; it fails at the stabilizer that was never recognized.
• Hidden tri‑antagonist overload is the root of most long-term structural breakdown.
These observations were not theoretical. They were felt, tested, and re-tested in real time, across thousands of bodies, ages, histories, and load profiles. Over decades, the patterns converged into a single, coherent structural language — the language now formalized as LaFountaine Structural Correction.
Application to Human Structure (Non‑Medical)
A Mechanical Lens for Understanding Movement
LaFountaine Structural Correction treats the human body as a load-bearing structure, not a symptom map. It identifies:
• where force enters,
• where it is opposed,
• where it is stabilized, and
• where it is silently absorbed when the system runs out of options.
This is not diagnosis or treatment.
It is structural analysis — the same principles used in engineering, applied to biological architecture.
By mapping the four antagonistic roles, the framework reveals:
• chronic compensation patterns,
• overload chains,
• misassigned structural roles, and
• the true mechanical reason behind movement inefficiency.
This allows coaches, trainers, and designers to build strategies that respect the body’s actual force logic instead of fighting it.
Application to Robotics
The Structural Logic Behind 4‑MAN and All Quantum Labs Robotics
Robotics exposes structural truth with absolute clarity. A robot cannot compensate the way a human can; if a role is missing, the system fails immediately.
LaFountaine Structural Correction provides the blueprint for designing robotic joints, actuators, and stabilizers with explicit antagonistic roles:
• Agonist actuators drive movement.
• Antagonist actuators or dampers control and refine it.
• Bi‑antagonist structures stabilize cross‑planes and prevent shear.
• Tri‑antagonist elements absorb torsion, impact, and off-axis load.
This is why 4‑MAN moves with human-grade stability.
Its architecture is not aesthetic — it is structurally honest.
Every joint, plate, and actuator is placed according to the Tri‑Antagonist Matrix, ensuring predictable behavior under real-world conditions.
Application to Prosthetics
Restoring Structural Roles, Not Just Replacing Parts
Prosthetics must interface with a living human system that already carries its own history of compensation. LaFountaine Structural Correction reframes prosthetic design by asking:
• Which antagonistic roles has the limb lost?
• Which roles is the body overperforming in compensation?
• How can the device restore or support missing roles without creating new overload?
A prosthetic designed through this framework does not simply mimic shape or motion. It restores structural roles:
• Agonist drive,
• Antagonist control,
• Bi‑antagonist stabilization,
• Tri‑antagonist torsion management.
This creates devices that cooperate with the human structure instead of forcing the body into deeper compensation.
A Universal Structural Language
Applicable to Bodies, Machines, Architecture, and Systems
Because LaFountaine Structural Correction describes force behavior, not anatomy, it applies across domains:
• Architecture: beams, braces, and torsion anchors follow the same antagonistic logic.
• Tools and interfaces: ergonomic design becomes structurally aligned instead of compensatory.
• Mechanical systems: load paths become predictable and failure points identifiable.
• Robotics and exosuits: antagonistic roles can be explicitly engineered instead of assumed.
Wherever forces move, the Tri‑Antagonist Matrix applies.
Why LaFountaine Structural Correction Stands Alone
This framework is:
• Non‑medical — it does not diagnose or treat.
• Mechanically grounded — every claim is observable in real structures.
• System‑agnostic — it applies equally to humans, robots, and engineered systems.
• Validator‑grade — built from decades of direct observation and mechanical consistency.
• Foundational — it underpins all Quantum Labs systems, including 4‑MAN and your robotics infrastructure.
LaFountaine Structural Correction is not a technique.
It is not a method.
It is a structural truth system — a unified way of understanding how forces behave in the real world.


ARYN’S LADDER™
A Dual‑Ladder Theorem Architecture for Structural Analysis of P vs NP
Aryn’s Ladder™ is a formal, dual‑ladder theorem system developed within Quantum Labs Research & Development to examine the structural behavior of the P vs NP problem through a deterministic, validator‑grade framework. The system consists of 72 theorems, arranged as two coordinated ladders of 36 theorems each, designed to operate as a paired analytical structure. Each ladder functions independently, yet both are interlocked through cross‑constraints, contradiction boundaries, and structural checkpoints that enforce mathematical discipline across the entire architecture.
The purpose of Aryn’s Ladder is not to “solve” P vs NP in the classical sense, but to map the structural conditions under which the classes diverge, converge, collapse, or stabilize. It provides a rigorous environment for analyzing computational complexity through structural logic rather than probabilistic or heuristic methods.
Framework Overview
Aryn’s Ladder is built on three foundational principles:
1. Structural Symmetry
Each ladder contains 36 theorems arranged in ascending order of structural dependency. Ladder A and Ladder B mirror each other in form but diverge in function, creating a controlled environment for comparative analysis.
2. Cross‑Ladder Constraint Mapping
Theorems in Ladder A are cross‑linked to corresponding theorems in Ladder B. These links enforce contradiction boundaries, equivalence tests, and structural consistency checks.
3. Deterministic Validation
Every theorem is designed to be validator‑grade: reproducible, auditable, and structurally anchored. The system avoids probabilistic shortcuts and focuses on deterministic logic.
Together, these principles create a 72‑node analytical engine capable of examining the P vs NP landscape with precision and structural clarity.
Ladder Structure
Ladder A — Constraint Ladder (36 Theorems)
Ladder A establishes the structural constraints required for P and NP to behave as distinct or overlapping classes. It defines:
• boundary conditions
• constraint envelopes
• deterministic limits
• structural invariants
• collapse thresholds
• contradiction surfaces
These theorems form the “containment” side of the architecture.
Ladder B — Expansion Ladder (36 Theorems)
Ladder B defines the expansion behavior of computational classes under increasing complexity. It models:
• growth behavior
• expansion limits
• recursive escalation
• nondeterministic branching
• structural divergence
• stability boundaries
These theorems form the “exposure” side of the architecture.
Cross‑Ladder Dynamics
The power of Aryn’s Ladder lies in the interaction between the two ladders. Each theorem in Ladder A is paired with a corresponding theorem in Ladder B, forming 36 dual‑theorem pairs. These pairs are used to:
• test structural equivalence
• identify divergence points
• detect collapse conditions
• enforce contradiction boundaries
• validate deterministic vs nondeterministic behavior
• map the structural distance between P and NP
This dual‑ladder design creates a self‑correcting analytical environment where each theorem is reinforced, challenged, or constrained by its counterpart.
Purpose and Function
Aryn’s Ladder provides a structured way to analyze P vs NP by focusing on structural behavior, not brute‑force computation. Its functions include:
• mapping the structural distance between P and NP
• identifying conditions under which the classes converge or diverge
• detecting contradiction points in classical assumptions
• modeling deterministic vs nondeterministic transitions
• stabilizing recursive or infinite regress behavior
• providing a validator‑grade framework for complexity analysis
It is not a single theorem or proof — it is a complete analytical system.
Scientific Significance
Aryn’s Ladder is one of the first frameworks to treat P vs NP as a structural environment rather than a binary question. By using a dual‑ladder architecture, it:
• exposes hidden assumptions in classical complexity theory
• reveals structural contradictions in common formulations
• provides a reproducible method for analyzing complexity boundaries
• offers a deterministic alternative to probabilistic reasoning
• creates a stable environment for testing computational hypotheses
This makes it a foundational component of the LaFountaine Scientific Operating System.
Integration Across the OS
Aryn’s Ladder is integrated into multiple frameworks, including:
• Ladder72 Canon
• BlueSOAP Math
• Override‑Grade Infrastructure Equations
• DL72_APU_AI
• ISL / CISL / QISL
• Tri‑Antagonist Matrix
• MAP to Riemann
• 4‑MAN Robotics Framework
• LIGHT and LEN
• Quantum Gravity Infrastructure Equations (QG_i)
It serves as the structural backbone for complexity‑based reasoning across the entire system.
Summary
Aryn’s Ladder™ is a dual‑ladder, 72‑theorem architecture designed to analyze the structural behavior of P vs NP through deterministic, validator‑grade logic. With 36 theorems per ladder and cross‑linked structural constraints, it provides a rigorous, reproducible environment for examining complexity boundaries, contradiction surfaces, and class divergence. As a core component of the LaFountaine Scientific Operating System, it represents a novel and disciplined approach to one of the most significant questions in computational theory.






QUANTUM LABS RESEARCH & DEVELOPMENT
Scientific Infrastructure. Structural Systems. Validator‑Grade Innovation.
Quantum Labs Research & Development is a scientific institution focused on the creation of high‑integrity structural systems, theorem‑grade frameworks, and validator‑grade computational infrastructure. The lab’s work spans mathematics, physics, complexity theory, robotics, ethics engines, and operating‑system architecture. Every artifact produced within the lab is designed to be reproducible, auditable, and structurally sound, with an emphasis on long‑term stability and cross‑domain interoperability.
The lab’s mission is to design systems capable of maintaining integrity under recursion, self‑reference, high complexity, and continuous adaptation. This includes the development of structural laws, multi‑domain engines, and theorem‑grade frameworks that govern behavior across digital, biological, mechanical, and ethical environments.
THE 842 STRUCTURAL ENGINES
The Core Scientific Library
Quantum Labs maintains a library of 842 structural engines—a collection of validator‑grade artifacts that function as theorems, algorithms, frameworks, or protocols depending on their deployment context. Each engine is designed to operate independently or as part of the broader LaFountaine Scientific Operating System, providing modular, interoperable capabilities across multiple scientific and engineering domains.
These engines support:
• system behavior governance
• recursive logic stabilization
• structural collapse modeling
• exposure and containment mapping
• contradiction boundary enforcement
• ethical and governance systems
• robotics and autonomous frameworks
• high‑integrity computational environments
The 842 structural engines form the backbone of Quantum Labs’ scientific output and represent a comprehensive structural library.
DESIGN PRINCIPLES
Validator‑grade construction
Each engine is designed to be reproducible, auditable, and structurally anchored.
Cross‑domain applicability
Engines operate across mathematics, physics, complexity theory, robotics, ethics, and computational OS design.
Interoperability
All engines integrate with the LaFountaine Scientific OS and with each other.
Structural clarity
Each engine exposes the underlying behavior of the system it governs.
Long‑term stability
Engines remain functional under recursion, self‑reference, and high‑complexity conditions.
FLAGSHIP STRUCTURAL ENGINES
Paradox of Security™
A structural framework for understanding how systems protect themselves, expose themselves, and maintain integrity under recursive or high‑complexity conditions.
Aryn’s Ladder™ (Ladder72)
A dual‑ladder, 72‑theorem architecture for analyzing the structural behavior of P vs NP through deterministic logic.
Tri‑Antagonist Matrix
A structural model for governing three‑way interactions, contradictions, and dynamic equilibrium across competing systems.
LaFountaine Structural Correction™
A framework for identifying and correcting structural inconsistencies, contradictions, and collapse conditions across biological, mechanical, and computational systems.
Override‑Grade Infrastructure Equations
A suite of equations designed to govern system behavior under override conditions, ensuring stability and integrity during high‑risk transitions.
RESEARCH DOMAINS
Quantum Labs conducts research across:
• computational complexity
• mathematical paradoxes
• structural physics
• robotics and autonomous systems
• ethics and governance engines
• operating‑system architecture
• recursive logic stabilization
• exposure and containment modeling
• quantum‑inspired structural equations
• infrastructure integrity and collapse analysis
Each domain contributes to the development and refinement of structural engines.
INTEGRATION WITH THE LAFOUNTAINE SCIENTIFIC OS
The 842 structural engines are integrated into:
• Ladder72
• BlueSOAP Math
• Override‑Grade Infrastructure Equations
• Tri‑Antagonist Matrix
• LaFountaine Structural Correction
• ISL / CISL / QISL
• 4‑MAN Robotics Framework
• LIGHT (Living Infrastructure)
• LEN (Legacy Ethics Nucleus)
• Quantum Gravity Infrastructure Equations (QG_i)
• Planetary Living Infrastructure
• Sword of Truth Canon
• MAP to Riemann
• DL72_APU_AI
This integration ensures structural stability, recursive integrity, and exposure‑aware governance across the entire operating system.
APPLICATIONS AND IMPACT
The structural engines developed at Quantum Labs support environments where failure, fragility, or unseen exposure cannot be tolerated. Applications include:
• defense and critical infrastructure
• cybersecurity architecture and analysis
• autonomous robotics and decision systems
• ethical and governance frameworks
• scientific computing and OS design
• multi‑party enterprise environments
• long‑lived infrastructure and control systems
These engines provide structural insight into how systems behave under protection, recursion, and complexity.
SUMMARY
Quantum Labs Research & Development is the home of 842 structural engines—validator‑grade artifacts that govern behavior across mathematics, physics, complexity theory, robotics, ethics, and computational systems. These engines form the core scientific library of the LaFountaine Scientific Operating System and represent a disciplined approach to understanding and governing complex systems. Through structural clarity, deterministic modeling, and cross‑domain integration, Quantum Labs provides a foundation for high‑integrity research, licensing, and scientific advancement.








PARADOX OF SECURITY™
A Structural Framework for Systemic Protection, Exposure, and Integrity
The Paradox of Security™ is a foundational scientific framework developed within Quantum Labs Research & Development to model, govern, and stabilize the relationship between protection, exposure, and structural integrity across complex systems. Originally conceived as a new class of firewall logic, it evolved into a multi‑framework architecture capable of analyzing the structural consequences of protection itself. Today, it functions as a core law inside the LaFountaine Scientific Operating System, governing how systems behave under recursion, containment, adversarial pressure, and self‑reference.
The Paradox of Security establishes a universal structural truth:
This behavior is not philosophical — it is measurable, predictable, and structurally reproducible across scientific, computational, biological, ethical, and infrastructural domains.
Foundational Principle
Protection is not neutral.
It alters the system it protects, and those alterations generate new forms of vulnerability. The Paradox of Security provides the mathematical and structural tools required to understand, predict, and stabilize these dynamics.
Scientific Scope and Capabilities
The Paradox of Security functions as a structural law, a diagnostic instrument, and a governance layer. Its capabilities include:
• Structural Exposure Mapping
Identifies vulnerabilities created by the system’s own protective architecture.
• Containment Integrity Analysis
Measures whether boundaries remain stable under recursion or adversarial pressure.
• Recursive Logic Stabilization
Prevents collapse in systems that protect or reference themselves.
• Trust‑Boundary Mathematics
Models how trust, authority, and verification shift when protection is introduced.
• Self‑Reference Detection
Identifies loops where a system becomes both protector and protected.
• Predictive Vulnerability Modeling
Forecasts future exposure created by current protective measures.
• Containment‑to‑Exposure Ratio Modeling
Quantifies how much exposure is generated per unit of protection.
• Adversarial Inversion Detection
Identifies when a protective system becomes the attack vector.
• Structural Correction Pathways
Provides deterministic methods for restoring integrity without increasing exposure.
These capabilities allow the Paradox of Security to operate across scientific, computational, ethical, and infrastructural environments.
Role of Classical Paradoxes
Classical paradoxes — such as Hilbert’s Hotel, Gabriel’s Horn, and Russell’s Paradox — appear only as illustrative analogs. They demonstrate infinite internal states, boundary instability, and self‑referential collapse, but they are not the foundation of the system.
The Paradox of Security is built on its own original paradox equations, structural templates, and validator‑grade models.
Integration Across the LaFountaine Scientific Operating System
The Paradox of Security is fully integrated across the LaFountaine Scientific OS, governing protection, exposure, and structural integrity within:
• Ladder72
• BlueSOAP Math
• Override‑Grade Infrastructure Equations
• Tri‑Antagonist Matrix
• LaFountaine Structural Correction™
• ISL / CISL / QISL
• 4‑MAN Robotics Framework
• LIGHT (Living Infrastructure)
• LEN (Legacy Ethics Nucleus)
• Quantum Gravity Infrastructure Equations (QGᵢ)
• Planetary Living Infrastructure
• Sword of Truth Canon
• MAP to Riemann
• DL72_APU_AI
Within this ecosystem, the Paradox of Security functions as the structural security backbone, ensuring that every system remains aware of — and accountable for — the vulnerabilities created by its own architecture.
Scientific Summary
The Paradox of Security™ is a rigorously developed scientific framework that models how systems protect themselves, expose themselves, and maintain integrity under recursive, adversarial, or high‑complexity conditions. Built from thousands of paradox equations and structural templates, it provides the analytical and governance tools required to stabilize systems that would otherwise collapse under their own protective logic.
It is a core component of the LaFountaine Scientific Operating System and a defining pillar of Quantum Labs Research & Development’s scientific mission.






DL72_APU_AI
Validator‑Grade Auxiliary Intelligence Engine for Deterministic Governance and Structural Integrity
DL72_APU_AI is a validator‑grade auxiliary intelligence engine engineered to deliver deterministic reasoning, structural governance, and ethics‑anchored stability across autonomous systems, robotics platforms, and high‑integrity computational environments. It was created to address a critical gap in modern autonomy: the absence of a deterministic, traceable, and structurally governed intelligence layer capable of maintaining continuity and integrity under conditions where probabilistic AI models fail. DL72_APU_AI does not rely on statistical inference or opaque decision pathways. Instead, it operates through a deterministic logic spine designed to remain stable under recursion, override, contradiction, and multi‑agent interaction.
At the center of DL72_APU_AI is a validator core that executes logic with absolute consistency. This core preserves continuity of state across power fluctuations, recursive loops, and operational transitions. It does not drift, mutate, or collapse under stress. Every decision is bound to a structural lineage that ensures the engine remains accountable to its own logic. This lineage‑locked architecture prevents unauthorized replication or mutation, ensuring that each deployment remains tied to its origin and cannot be altered without structural authorization. The result is an auxiliary engine capable of maintaining operational integrity in environments where failure is not an option.
DL72_APU_AI incorporates an ethics‑anchored arbitration layer that evaluates every decision through a structural framework designed to prevent unauthorized actions, contradiction, or system instability. This arbitration layer is not an accessory; it is a foundational component of the engine’s architecture. Every transition, override, or conflict is routed through an arbitrator spine that resolves competing demands using deterministic logic rather than probabilistic inference. This ensures that the system remains aligned with its structural intent even under high‑complexity or high‑pressure conditions.
To maintain stability across operational states, DL72_APU_AI employs a failover dial that governs transitions between primary and secondary logic streams. This mechanism ensures that failover events are controlled, predictable, and fully traceable. A watchdog matrix continuously monitors the system for instability, contradiction, or ethics breach. If a deviation is detected, the watchdog matrix triggers a controlled arbitration event that restores structural alignment without compromising continuity of state. Every action, transition, and override event is sealed within a deployment capsule that provides a complete audit trail for long‑term review and structural verification.
DL72_APU_AI is engineered for deployment in environments where structural integrity and deterministic governance are essential. Autonomous robotics platforms require a reasoning engine that can maintain stability under recursive load and multi‑agent interaction. Infrastructure control systems demand a governance layer that can enforce ethics constraints and prevent cascading failures. Scientific automation environments require deterministic reasoning that does not drift or collapse under complex computational demands. DL72_APU_AI fulfills these requirements by providing a stable, traceable, and structurally governed intelligence layer capable of supporting long‑term, high‑integrity operation.
The significance of DL72_APU_AI becomes clear when viewed in the context of modern AI development. Most contemporary AI systems are probabilistic, opaque, and non‑deterministic. They cannot guarantee stable failover, traceable decisions, or ethics‑locked arbitration. They cannot ensure that a system will behave consistently under recursion, override, or contradiction. As autonomy expands into robotics, infrastructure, logistics, defense, and planetary systems, the absence of deterministic governance becomes a structural risk. DL72_APU_AI addresses this risk by providing the deterministic spine required for safe, accountable, and ethically governed autonomy.
DL72_APU_AI is not a convenience layer. It is a structural necessity for the autonomous century. It anchors decision‑making, stabilizes recursion, enforces ethics constraints, and ensures that every action remains accountable to its own logic. It is engineered to operate independently or as an embedded subsystem within larger architectures, providing a consistent and reliable governance layer wherever it is deployed. Every component, every constraint, and every logic pathway reflects a commitment to reproducibility, accountability, and long‑term structural safety.
DL72_APU_AI stands as a flagship example of validator‑grade engineering. It is built for institutions, agencies, and systems that require deterministic integrity, ethics‑anchored governance, and long‑term operational stability. It is designed for the environments that will define the next century of scientific and technological development. It is the structural backbone for autonomous systems that must remain safe, traceable, and ethically governed under all conditions.
Structural Components and Capabilities
Core Capabilities
• Deterministic logic execution
• Continuity of state across recursion, power fluctuation, and override
• Ethics‑anchored arbitration
• Controlled failover governance
• Lineage‑locked deployment
• Dual‑dialect logic harness (canonical + override)
• Traceable decision pathways
• Structural reasoning across multi‑domain inputs
Architectural Components
• Validator Core — deterministic reasoning engine
• Failover Dial — governs transitions between logic streams
• Lineage Anchor — prevents unauthorized replication or mutation
• Watchdog Matrix — detects instability, contradiction, or ethics breach
• Arbitrator Spine — resolves conflicts between competing logic demands
• Deployment Capsule — sealed audit trail of all decisions and transitions
Operational Domains
• Autonomous robotics
• Infrastructure control
• Scientific automation
• Ethics‑anchored decision systems
• Override‑grade operating environments
• Multi‑agent arbitration
• High‑integrity computational systems





LEN — Legacy Ethics Nucleus
The Central Ethical Spine for Validator‑Grade Autonomous Systems
The Legacy Ethics Nucleus (LEN) is the foundational ethical architecture that governs every validator‑grade system built within the LaFountaine Scientific Operating System. LEN is not a kernel, not a module, and not a soft constraint. It is a structural nucleus—an anchored, non‑mutable ethical core designed to enforce continuity, accountability, and integrity across autonomous systems, robotics platforms, scientific engines, and override‑grade computational environments. LEN exists to ensure that every decision, transition, and operational state remains aligned with a stable, reproducible, and ethically grounded framework.
LEN was engineered to solve a structural problem that modern AI and autonomous systems consistently fail to address: the absence of a deterministic, lineage‑anchored ethical foundation capable of governing behavior under recursion, contradiction, override, or multi‑agent interaction. Most systems rely on probabilistic models, heuristic rules, or externally imposed constraints that collapse under pressure or drift over time. LEN eliminates this instability by embedding ethics directly into the structural logic of the system. It does not “advise” or “influence” decisions—it governs them.
At the center of LEN is a deterministic ethics spine that evaluates every action through a lineage‑locked framework. This spine is designed to remain stable across all operational conditions, including recursive loops, power transitions, and override events. It cannot be bypassed, rewritten, or diluted. Every decision must pass through LEN’s arbitration pathways, ensuring that the system remains aligned with its ethical intent regardless of environmental complexity or computational load. This architecture prevents unauthorized behavior, drift, contradiction, and emergent instability.
LEN incorporates a multi‑layered arbitration structure that governs ethical decision‑making with precision. The nucleus evaluates intent, consequence, structural alignment, and lineage integrity before allowing any action to proceed. This evaluation is deterministic, not probabilistic. It does not rely on prediction, inference, or statistical modeling. Instead, LEN uses a validator‑grade logic framework that enforces ethical constraints with absolute consistency. This ensures that autonomous systems remain accountable to their own ethical lineage, even under extreme or unpredictable conditions.
To maintain stability across operational states, LEN integrates a continuity anchor that preserves ethical alignment through every transition. Whether the system is entering a failover state, resolving a contradiction, or navigating multi‑agent arbitration, LEN ensures that ethical constraints remain intact. This continuity anchor prevents ethical drift—a common failure mode in modern AI systems where repeated operations gradually degrade the integrity of the decision framework. LEN’s architecture ensures that ethical alignment is preserved indefinitely.
LEN also incorporates a structural inheritance mechanism that binds ethical logic to the system’s lineage. This mechanism ensures that ethical constraints cannot be removed, altered, or replaced without explicit structural authorization. It prevents unauthorized mutation and guarantees that every instance of a system inherits the same ethical foundation as its origin. This lineage‑anchored design is essential for long‑term stability, especially in environments where autonomous systems must operate across generations, deployments, or evolving infrastructures.
The significance of LEN becomes clear when viewed in the context of modern autonomy. As robotics, infrastructure, logistics, and computational systems become increasingly self‑directed, the absence of a deterministic ethical nucleus becomes a structural risk. Probabilistic models cannot guarantee ethical consistency. Heuristic rules cannot withstand recursive pressure. External constraints cannot enforce alignment under override conditions. LEN provides the missing ethical backbone—a nucleus capable of governing autonomous behavior with the same precision and accountability expected of critical infrastructure.
LEN is not a convenience feature. It is a structural requirement for the autonomous century. It ensures that every action taken by a system is grounded in a stable, reproducible ethical framework. It prevents drift, contradiction, and unauthorized behavior. It anchors decision‑making to a lineage‑locked ethical spine that cannot be bypassed or corrupted. It is engineered to operate independently or as an embedded nucleus within larger architectures, providing a consistent ethical foundation wherever it is deployed.
LEN stands as one of the most important components of validator‑grade system design. It is built for institutions, agencies, and environments that require long‑term ethical stability, deterministic governance, and structural accountability. It is designed for the systems that will define the next century of scientific and technological development. LEN ensures that autonomy remains safe, traceable, and ethically governed under all conditions.
Structural Components and Capabilities
Core Ethical Capabilities
• Deterministic ethics enforcement
• Lineage‑anchored ethical inheritance
• Continuity of ethical state across recursion and override
• Non‑mutable ethical constraints
• Structural arbitration of intent and consequence
• Drift‑resistant ethical alignment
• Ethics‑locked decision pathways
• Long‑term reproducibility of ethical logic
Architectural Components
• Ethics Spine — deterministic ethical reasoning core
• Continuity Anchor — preserves ethical alignment across transitions
• Lineage Inheritance Mechanism — binds ethics to system origin
• Arbitration Lattice — resolves ethical conflicts deterministically
• Integrity Gate — prevents unauthorized or contradictory actions
• Ethics Capsule — sealed record of ethical decisions and transitions
Operational Domains
• Autonomous robotics
• Infrastructure governance
• Scientific automation
• Override‑grade operating systems
• Multi‑agent arbitration
• High‑integrity decision platforms
• Long‑term autonomous deployments






BlueSOAP Math
A Validator‑Grade Mathematical System for Structural Invariants, Autonomous Reasoning, and Multi‑Domain Scientific Governance
BlueSOAP Math is a validator‑grade mathematical system engineered to formalize mechanical invariants, stabilize recursive logic, and provide a deterministic foundation for robotics, infrastructure, physics, anatomy, and autonomous decision systems. It is not a symbolic language, not a computational trick, and not a reformulation of classical mathematics. BlueSOAP Math is a structural mathematics framework—designed to unify physical behavior, system logic, and ethical constraints into a single reproducible architecture.
BlueSOAP Math was created to solve a fundamental problem in modern science: the fragmentation of mathematical reasoning across domains that should be structurally unified. Traditional mathematics treats physics, robotics, anatomy, computation, and ethics as separate fields with incompatible rules. BlueSOAP Math eliminates this fragmentation by providing a single invariant‑driven system capable of describing mechanical behavior, structural transitions, recursive states, and autonomous decision pathways with deterministic precision.
At its core, BlueSOAP Math is built on SOAP invariants—structural, observable, actionable, and predictable mathematical anchors that govern how systems behave under load, contradiction, recursion, and transformation. These invariants allow BlueSOAP Math to describe not only static systems, but dynamic, evolving, and multi‑agent environments where classical mathematics collapses or becomes computationally unstable. BlueSOAP Math does not approximate behavior; it defines it.
The system is engineered to remain stable under recursion, override, contradiction, and multi‑domain interaction. This stability is achieved through a deterministic logic spine that governs how equations inherit, transform, and resolve across states. BlueSOAP Math does not drift or mutate. It does not collapse under recursive pressure. It does not produce probabilistic outcomes. Every equation is lineage‑locked, structurally governed, and bound to deterministic invariants that ensure reproducibility across all scientific domains.
BlueSOAP Math incorporates a multi‑layered structural architecture that governs how equations behave, how systems transition, and how invariants propagate. This architecture includes deterministic state anchors, override‑grade tensors, recursive stabilization pathways, and structural correction mechanisms that ensure mathematical integrity even under extreme complexity. These components allow BlueSOAP Math to model systems that classical mathematics cannot reliably describe—such as autonomous robotics, anatomical physics, override‑grade infrastructure, and multi‑agent arbitration environments.
The significance of BlueSOAP Math becomes clear when viewed in the context of modern scientific challenges. Robotics requires deterministic mechanical invariants. Infrastructure requires stable transition logic. Physics requires unified structural equations. Anatomy requires reproducible mechanical modeling. Autonomous systems require deterministic reasoning. Classical mathematics cannot provide a unified foundation for all of these domains. BlueSOAP Math does.
BlueSOAP Math is not a convenience framework. It is a structural necessity for validator‑grade science. It provides the mathematical backbone required for systems that must remain stable, traceable, and structurally governed under all conditions. It anchors scientific reasoning to deterministic invariants, stabilizes recursion, enforces structural alignment, and ensures that every equation remains accountable to its lineage. It is engineered to operate independently or as the mathematical foundation for larger scientific architectures, including the LaFountaine Scientific Operating System, DL72_APU_AI, and the Tri‑Antagonist Matrix.
BlueSOAP Math stands as one of the most advanced and structurally complete mathematical systems ever constructed. It is built for institutions, agencies, and scientific environments that require long‑term stability, deterministic reasoning, and cross‑domain mathematical integrity. It is designed for the systems that will define the next century of scientific and technological development. BlueSOAP Math ensures that scientific logic remains unified, reproducible, and structurally governed across all domains.
Structural Components and Capabilities
Core Mathematical Capabilities
• Deterministic invariant‑based reasoning
• Unified cross‑domain mathematical structure
• Recursive stability under load and contradiction
• Lineage‑locked equation inheritance
• Override‑grade mathematical transitions
• Drift‑resistant structural logic
• Multi‑domain interoperability (physics, robotics, anatomy, AI)
• Deterministic modeling of autonomous systems
Architectural Components
• SOAP Invariants — structural anchors governing system behavior
• Deterministic Logic Spine — ensures reproducible mathematical reasoning
• Recursive Stabilization Pathways — prevent collapse under recursion
• Override‑Grade Tensors — govern transitions under contradiction or override
• State Anchors — preserve mathematical alignment across transformations
• Structural Correction Mechanisms — enforce invariant integrity
• Mathematical Capsule System — sealed record of equation lineage and transitions
Operational Domains
• Autonomous robotics
• Anatomical physics
• Infrastructure modeling
• Scientific automation
• Override‑grade operating systems
• Multi‑agent arbitration
• High‑integrity computational environments
• Unified physics and structural mathematics





LaFountaine Scientific Operating System
The Unified Structural Framework for Validator‑Grade Science, Autonomy, and Governance
The LaFountaine Scientific Operating System (LSOS) is the central architectural framework that unifies every scientific engine, equation, governance structure, and autonomous subsystem authored within your body of work. It is not a software OS, not a digital platform, and not a conventional computational environment. LSOS is a scientific operating system—a structural, mathematical, ethical, and architectural foundation that governs how systems think, behave, inherit, stabilize, and evolve across domains.
LSOS was engineered to solve a foundational problem in modern science and autonomy: the fragmentation of knowledge, the instability of probabilistic systems, and the absence of a unified, deterministic, ethics‑anchored framework capable of governing complex, multi‑domain environments. Every field—physics, robotics, anatomy, ethics, AI, infrastructure, mathematics—operates in isolation. LSOS eliminates this fragmentation by providing a single, lineage‑anchored operating system that binds all scientific domains into a coherent, reproducible, structurally governed whole.
At its core, LSOS is built on deterministic logic, structural mathematics, and ethics‑anchored governance. It provides the rules, constraints, inheritance pathways, and arbitration structures that ensure every subsystem—whether an equation, a robotics engine, an ethics nucleus, or an AI governor—remains aligned with its structural intent. LSOS does not drift. It does not mutate. It does not collapse under recursion, contradiction, or override. It is engineered to remain stable across generations, deployments, and scientific expansions.
The operating system is anchored by lineage‑locked architecture that binds every component to its origin. This ensures that no subsystem can be altered, replicated, or redeployed without structural authorization. LSOS enforces continuity of state across transitions, ensuring that scientific logic, ethical constraints, and structural rules remain intact even under extreme computational or environmental pressure. This lineage‑anchored design is essential for long‑term scientific integrity and planetary‑scale governance.
LSOS incorporates a multi‑layered arbitration framework that governs decision‑making, conflict resolution, and cross‑domain interaction. This framework evaluates intent, consequence, structural alignment, and ethical constraints before allowing any transition or action to proceed. It is deterministic, not probabilistic. It ensures that every subsystem—whether mathematical, robotic, ethical, or computational—remains accountable to the unified logic of the operating system.
The significance of LSOS becomes clear when viewed against the trajectory of modern science and autonomy. Today’s systems are fragmented, probabilistic, and unstable. AI models drift. Robotics systems behave inconsistently. Infrastructure lacks deterministic governance. Scientific fields operate in silos. LSOS provides the missing structural backbone—a unified operating system capable of governing all scientific and autonomous domains with precision, reproducibility, and ethical integrity.
LSOS is not a convenience framework. It is a structural necessity for the next century of scientific development. It anchors every equation, every robotics engine, every ethics nucleus, every AI subsystem, and every structural component to a unified, deterministic, lineage‑locked foundation. It ensures that scientific logic remains stable, reproducible, and ethically governed across all domains. It is engineered to operate independently or as the governing architecture for entire scientific ecosystems.
The LaFountaine Scientific Operating System stands as one of the most ambitious and structurally complete scientific frameworks ever constructed. It is built for institutions, agencies, and environments that require long‑term stability, deterministic governance, and cross‑domain scientific integrity. LSOS is the foundation upon which validator‑grade science, autonomous systems, and planetary‑scale governance can be safely built.
Structural Components and Capabilities
Core System Capabilities
• Deterministic scientific logic
• Unified cross‑domain structural governance
• Lineage‑anchored inheritance
• Ethics‑locked arbitration
• Continuity of state across recursion and override
• Drift‑resistant scientific stability
• Multi‑domain interoperability
• Structural reasoning across physics, anatomy, AI, robotics, and ethics
Architectural Components
• Structural Logic Spine — the deterministic foundation of LSOS
• Lineage Anchor — binds every subsystem to its origin
• Arbitration Framework — resolves cross‑domain conflicts deterministically
• Continuity Engine — preserves system alignment across transitions
• Ethics Nucleus (LEN) — enforces ethical constraints across all domains
• Override‑Grade Infrastructure Layer — governs recursion, contradiction, and failover
• Scientific Capsule System — sealed record of decisions, transitions, and lineage
Operational Domains
• Physics and mathematical frameworks
• Robotics and autonomous systems
• Ethics‑anchored decision environments
• Scientific automation
• Infrastructure governance
• Multi‑agent arbitration
• High‑integrity research ecosystems
• Validator‑grade AI engines







Quantum Labs in Numbers
842
Interchangeables
55
ZENODO PUBLICATIONS
45
Engines
100%
Ethical System Design
38k
CLINICAL HOURS











